曼彻斯特大学教授J.M.Currie 1981年发表在剑桥大学出版社理论著作The Economic Theory of Agricultural Land Tenure(《农地租赁的经济理论》)第一次完整地归纳了不同地区间各种农地使用权或租赁形式的特点,并在新古典经济学的基础上结合Nakajima(1970)年“新古典的农户效用最大化理论模型”构建了农地租赁的理论分析框架。
《农地租赁的经济理论》(后文简称“农地租赁理论”)涉及到了农场主土地自耕(owner-occupancy)情况下的农业投资决定、农地租赁(tenancy)情况下的农业投资决定、固定租金条件下的农地租赁市场、按收定租条件下的农地租赁市场、农地租赁与非农就业等相关领域的分析和模型,并结合英国农地的具体实践进行了案例分析,提出了评估农地价值和租赁效率的理论判断。本文将讨论“农地租赁理论”中农户非农就业与农地租赁关系的分析框架。
农户在耕种农地时需要耗费劳动,除此之外,假设农户拥有的如牲畜、种子和其它设备都是固定的,并且生产出来的所有农产品除了一部分自己消费外其它全部用于出售,且购买生产资料的渠道仅在专门的市场,这就限定了其他商品无法进入农户的生产生活,也就无法替代为了生产的而进行的原材料的必要投入。另外,暂时不考虑村民资本信贷的需求。最后,再假设所有的非劳动的因素都是固定的,农户对所有与土地相关的原材料和农产品的价格都是已知并由市场给定。
先考虑最简单的没有非农就业时的情况。令代表在t时间时投入农业的劳动,令代表在t+1时间点获得的在上个t时间段收获的农产品的总收入。总收入与劳动之间的关系取决于农户劳动的方式、生产的具体商品,但是农户会在已投入劳动的情况下最大化农业总收入
上式的具体形式取决于农户拥有的非劳动因素、生产不同农作物的技术水平以及最终农产品的价格。假设劳动的边际收入产出为正,但边际递减。
在t+1时间点,农户不仅要决定投入的劳动,还要确定下个t时间段的消费支出,假设借贷行为无发生,且农户的消费支出只受到t时间开始时金融资产
农户最终的金融资产包括从农作物销售获得的现金以及农户存款,另外,农户在t+1时间段结束时可能会获得一笔来源于农作物生产以外的其它收入,当然这笔钱也可能是准备在某时间需要上缴的税费等。令代表这笔其它的收入或预备支出的净值,那么
农户的效用可以用一个可微的,严格凹的效用函数表示:
在上式中,当消费支出和最终金融资产递增,同时劳动减少的时候,农户效用是严格增加的。该式子的具体形式与农户的人口结构密切相关,尤其是家庭中的劳动力数量以及无劳动能力者(dependents)的数量(Sen,1966;Nakajima,1970)。式中,且小于农户总的劳动力。
农户总收入最大化要求需要选择一个消费支出与劳动的投入组合,解决的途径有:首先,劳动收入的边际贡献与最终金融资产之比应该等于金融资产与闲暇的边际替代率;第二,消费与最终金融资产的边际替代率等于1;第三,消费与闲暇的边际替代率应该等于劳动的边际收入产品。
因此,从简单化模型的角度出发,我们假设农户将初始的金融资产全部用于消费,即,这个假设并不是随意的数学简化,因为在现实生活中处于贫困地区的农户可能并不会去考虑如何分配本已经很少的金融资产(即很少的现金)以增加效用,而会考虑“有多少钱花多少钱”,因此这个假设也是有意义的,基于这个假设,图1表示了在没有农地租赁情况下农户的劳动—金融资产选择。
图1中, 表示了农户在投入一定劳动后的农户金融资产,截距OX代表了其它净收入。每条无差异曲线I代表在给定的消费支出后,劳动与金融资产的组合带来的效用是无差异的,同时无差异曲线的斜率为正表示金融资产的增加需要相应的劳动的增加来实现。代表劳动与金融资产的组合带来的效用高于,农户的最大效用发生时需要金融资产-劳动曲线刚好与能够获得的最高的无差异曲线(图上为)相切,切点为(),即在获得最大效用时劳动的投入为,相应的金融资产为。
从上图中,我们可进一步分析。首先,假设其它的净收入增加,其带来的图中的效果不确定;但是如果金融资产和闲暇保持稳定的话,增加会导致劳动投入的减少,也即闲暇会相应增加,最终实现期末金融资产的增加。这意味着,对土地征税的行为会增加农户的工作量。第二,在非劳动力因素和技术水平没有发生变化时,农业收入与劳动投入关系的变化可能导致农作物价格水平发生变化。总的来说,其他总收入提高带来的直接效果是不确定的。如果农户人口规模扩大,那么随之而来的边际收入产品会增加,可能对劳动起到替代效应;但是,金融资产的增加又会降低劳动投入——两种反方向作用会导致劳动投入发生提高或降低两种不同的变化。
接下来考虑农户有选择非农就业的可能性。假设农户在给定的非农工资率w条件下可以自主选择投入到非农行业的期限和劳动量,其中非农工资在每个时间段末期发放。则最后的金融资产可以表示为:
其中代表总的劳动,代表从事农业的劳动数量,则代表非农就业的劳动量,代表给定的非农就业工资率。
农户不仅需要选择要投入的劳动总量,还要考虑分配在农业和非农业两方便的劳动量。假设农户从事两种行业的劳动是同质的,效用最大化的前提就是在总劳动量的投入一定时获得最大的收益。当农户既从事农业又从事非农业时,效用最大化的必要条件是两种工作情况下的期末金融资产边际贡献率相等,因此农业劳动的边际收入产品应该等于非农就业的工资率,后者体现了劳动力在非农行业就业时的边际机会成本。


图 2 存在非农就业机会时农户劳动的分配决策示意图
代表了在任何劳动水平上农户可能实现的期末金融资产的最大值,其中的斜率等非农就业的工资率w,且与相切于点,代表农业劳动的边际收入产品与非农就业的工资率相等。假设农户在做出最优选择时的劳动总量为,其中为投入的农业劳动,则()即为非农就业的劳动量,对应的最终金融资产为,满足()=.
在考虑非农就业的情况下,农户对于劳动分配的选择有了较大的变化。首先,非农就业工资率的提高会降低农户投入农业中劳动的比例,如果非农行业工资率足够高时,农户就会理性地放弃农业生产,而将劳动全部投入到非农行业当中,这就意味着农户耕种的土地有可能被荒废或被租出;其次,某些因素,如土地规模的扩大、生产技术水平的提高等都可能对最终的结果产生影响。定性地来看,土地规模的扩大将会导致投入到农业劳动的边际收入产品增加,也就可能使更多的劳动被用于农业生产,假设土地规模扩大最终带来了规模化经营,且边际收入产品足够大时,农户的劳动就将理性地倾斜到农业生产,甚至选择放弃非农就业。由此可见,在讨论农户劳动的分配时,农地是非常重要的因素,接下来将进一步讨论存在农地租赁时,劳动在农业与非农行业的分配情况。
在上文讨论的基础上,接下来将继续探讨发生农地租赁时决定农地是由农户自己耕种还是将其出租的因素及影响机制。假设农户在发生农地租赁时土地租金是通过现金支付,并且在每个时期内租金为固定值(该假设与中国农村的实际情况一致,在调研中很少发现地租是由最终的农业产出按一定比例计算),同时农地的所有权(或农地承包经营权)是预先确定的且农地经营权不存在争议。此外,考虑到边际规模问题,模型中的农地不可进一步分割为小块土地,且同一租出者租赁的土地是同质的。在土地租入者在支付一笔固定的现金后即获得了一定时期内所租赁土地的使用权,在租期结束后租赁自动结束,当然双方也可续签租赁协议。假设每一个租赁期限都为1年,地租在每一租赁期结束时交付,且租赁行为不会对农地的生产能力产生影响。
接下来的模型中会引入两个概念[③]——农地租出者能够接受的最低租金(reservation price)和租入者愿意承担的最高地租(limit price)。简单来说,指农户在考虑租入其他农户土地时能够承受的地租的最大值;而指土地所有者愿意接受的能够租出土地的最小值。
租入者愿意承担的最高地租(limit price),它是指农户如果在不进入农地租赁市场时通过在其他可以进入的行业劳动所能获得的效用,当农户租入土地时所支付的租金等于时所获得的效用与上述效用相等,也即只有当农户支付的实际地租小于时,才能获得大于租入土地的机会成本带来的效用。
令农户不租赁土地而在其他行业所能获得的最大效用,()代表农户支付租金时在农业生产方面所能获得的效用,则
()=
与农户在非农市场上从事任一职业时所能获得的最高工资率紧密相连,我们假设农户会将最初的金融资产全部用于消费,且农户不从事农业生产时最有选择的职业的工资率是,则如图所示,OB的斜率与非农就业的工资率相等,代表了农户在选择非农就业时能够获得的效用(OB与),在图中农户选择投入于农业劳动,则相应能够获得的期末金融资产为,此时()位于无差异曲线上,OX表示当地租为0时的各种投入农业的劳动与期末金融资产的组合(此时OX与有交点,意味着在两个交点间的组合都能让农户获得的效用,因此农户是愿意租入土地的),我们将OX曲线平移至处,令于,此时与纵轴交于Y点,此时OY即为租入者愿意承担的租赁农地的最高租金(limit price)。可以看出,取决于农户从事农业劳动时相比非农就业所能获得的产出,非农行业的工资率越高,农户愿意承担的最高地租就越低。

农地租出者能够接受的最低租金(reservation price),指农户不在某块土地进行农业生产时,将该土地交由其他人管理而能收获的最低收入。比如,农户请A代为管理自己的土地,该地块生产出来的农产品卖出后的收入减去成本,再减去给A的管理费,即为期末农户从该土地得到的收入。考虑到农户可请A管理土地,也可请B、C……等管理,则农户请任何管理者经营土地后获得的最低的收入即为该农户接受的最低租金。一种极端情况是没有人愿意替农户管理土地,而农户自身也不愿意花费精力来管理土地,则此时租出者能够接受的最低租金为0。
当然,农户在请人管理土地后的预期收益与租赁土地的租金相等时,该农户更愿意选择租出土地,因为预期的收益是不确定的,而土地的租金已在租赁发生时约定好,因此后者的风险更小。
农地租赁的实现条件。在开始分析农地的租赁模型时,先假设进入农地租赁市场的成本为0,同时在该市场中有足够的农户等待完成土地的租入或者租出。当然最简单的情况是该市场中只有一个土地租出者和一个土地租入者。
只有当实际发生的土地租金介于农地租出者能够接受的最低租金与租入者愿意承担的最高地租之间时,租赁才有可能发生,即,由租赁双方在该范围内协商谈判确定。一种特殊情况是,当时,理论来讲租赁应该会发生,但是在这种情况下双方从自身来说租赁与否并不重要,因此从实际上来说此时租赁也有可能不发生。
如果市场上出现了一个租出者和两个租入者,则此时令租出者能够接受的最低租金依然为,而两个租入者A和B愿意承担的最高地租分别为和,且>,在这种情况下农地将会被租给A,但是B由于缩小了该农地租赁实现的地租范围,最终的租金会满足。
如果=,则农地将会被租给A或者B中的其中一位,并且由于存在竞争,最终的租金将会等于A和B愿意承担的最高地租,但是最终给A还是B是不确定的。
考虑租赁市场上存在两位租出者和两位租入者的情况,假设在发生租赁时的市场中的租金是完全一样的,令和表示租出者X和Y能够接受的最低租金,和代表租入者A和B愿意承担的最高租金,A和B情况完全相同,X和Y情况完全相同,且,则最终发生的租赁价格的区间一定为
上述过程可以用图4所示,其中农地租出方的供给阶梯函数为,农地租入方的需求阶梯函数为,最终实现租赁的地租范围为,也即X和Y的土地将以相同的地租完成租赁,地租价格大于X能够接受的最低租金,小于B愿意承担的最高租金。
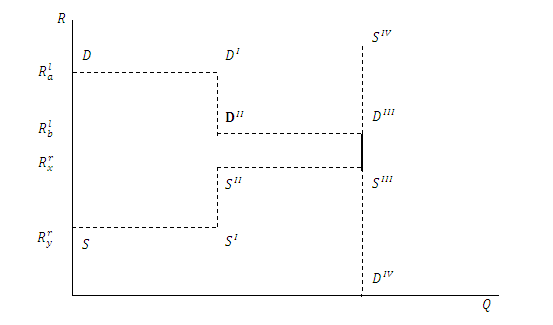
最后,我们将进入农地租赁市场的租出者的数量扩大到m人,租入者的数量扩大到n人,令 表示第i个农地租入者(i=1,2,3,…,m)愿意承担的最高租金,表示第j个农地租出者(j=1,2,3,…,n)能够接受的最低租金。假设≤≤≤≤,,同时为了保证肯定能够发生农地租赁的情况以便于分析,令>,且最终在农地租赁市场中完成租赁的地租全部相等,最终实际发生了k个农地租赁,则
Max() min()
在两租出者、两租入者模型中,可以分别构建租出者的供给阶梯函数和租入者的需求阶梯函数,在现在构建的多租出者、多租入者模型中,也可以构建相应的供给阶梯函数和需求阶梯函数。需要注意的是,由于在事先假设中租出者的土地是不可分割的,因此最终实现租赁协议的个数也是不确定的,这种情况不会伴随着进入市场的租出者和租入者的数量的增加而消失,但可以认为由于农地租赁市场中双方数量增加,可供租赁匹配的可能性得以增加。在将租出者和租入者的数量假设为足够多时,可以用平滑的曲线来表示上述分析过程,如图8所示,DD代表租入者的需求曲线,代表租出者的供给曲线,则最终能够实现的地租价格为,有数量的农地完成了租赁,的土地未能完成租赁,只能由准备出租农地的农户自己耕种,或交由其他人代为管理。
我们可以预期,当发生农地租赁后,原来从事农业生产的劳动力(或剩余劳动力)将会选择新的就业机会,而理性的劳动者将选择报酬率更高的非农行业。

| |
[①]J.M. Currie(1981).The economic theory of agricultural land tenure .New York :Cambridge University Press:51-56.
[②]J.M. Currie(1981).The economic theory of agricultural land tenure .New York :Cambridge University Press:81-91.
[③]此概念最早出自“协作博弈论”(Theory of co-operative games)中处理简单贸易情形下的效用转移,见Von Neumann & Morgenstern(1944); Telser(1972); Bacharach(1976)等学者的著作。
.png?20211108)







